如何优雅地进行质因数分解
在本文中 我们将列举一些质因数分解的方法 请默认下文中的$n$是待分解的数
下面列举的分解方式有快有慢 有些算法在分解一个大质数的时候会非常慢 比如Fermat's factorization method Pollard rho 所以我们有必要在分解之前做一次素性测试 当然 对于大数 我们应该使用快速的素性检测算法
我们将先介绍常用的检测算法Miller–Rabin primality test作为前置知识 然后开始本文的主要内容
Miller–Rabin primality test
这是一种概率性的素性检测方式 依赖于费马小定理和一个引理 我们先来复习一下费马小定理: $$ \text{如果 p是一个质数 而且}p > 2 \ ,\text{则} a^{p-1}\equiv1\ (mod\ p)\text{对任意a满足}gcd(a,p)=1\text{成立} $$ 用的引理是:
当$p$是一个素数 而且$p > 2$时 1在模p意义下不存在非平凡的平方根
我们先阐述一下平凡的定义:由于对于$n\in N$ 都有$(-1)^2\equiv 1\ (mod\ n)$ 和 $1^2\equiv 1\ (mod\ n)$ 所以1和-1是平凡的平方根
下面将证明这个引理:
Proof: $$ \text{我们假设}x\text{是}1\text{在模p意义下的一个非平凡平方根,p是奇质数}\\ x^2\equiv 1\ (mod\ p)\\ (x-1)(x+1)\equiv0\ (mod\ p)\\ \text{即}p|(x-1)(x+1)\\ \text{根据欧几里得引理得到:}p|x-1\text{或}p|x+1\\ \text{此时}x\text{必然是平凡平方根,与题设矛盾,所以引理成立}\\ $$ 接下来解释一下算法的原理:
我们现在有一个奇素数$n$ 并选定一个底数$a,\ gcd(a,n)=1$ 我们表示成费马小定理的形式: $$ a^{n - 1}\equiv 1\ (mod\ n) $$ 我们考虑将$n - 1$表示成$2^st,\ s,t\in N, t\equiv 1\ (mod\ 2)$
那么根据那个引理 1在模$n$下没有非平凡平方根 所以对于任意$r\in[0,s-1]$ 满足: $$ a^{d}\equiv 1\ (mod\ n)\\ a^{2^rd}\equiv -1\ (mod\ n)\\ $$ 所以我们一旦找到一个$a$ 使得上式均不满足 那么他不然不是素数
代码实现:
int mul(int a,int b,int mod)
{
int tmp = a * b - (int) ((long double) a * b / mod + 0.5) * mod;
return tmp < 0 ? tmp + mod : tmp;
}
int ksm(int a,int b,int mod = mod)
{
int res = 1;
while (b)
{
if (b & 1) res = mul(res,a,mod);
a = mul(a,a,mod);
b >>= 1;
}
return res;
}
int check(int a,int n)
{
int b = (n - 1),k = 0;
while (!(b & 1))
{
b >>= 1;
k++;
}
int res = ksm(a,b,n);
if (res == 1 || res == n - 1) return 0;
while (k--)
{
res = mul(res,res,n);
if (res == n - 1) return 0;
}
return 1;
}所以我们可以得到Miller–Rabin的板子:
int Miller_Robin(int n)
{
if (n == 2 || n == 3 || n == 5 || n == 7 || n == 11 || n == 13 || n == 17 || n == 19) return 1;
if (n == 23 || n == 29 || n == 31 || n == 37 || n == 41) return 1;
if (n == 46856248255981ll) return 0;
if (n < 2 || !(n & 1)) return 0;
if (!(n % 3 && n % 5 && n % 7 && n % 11 && n % 13 && n % 17 && n % 19)) return 0;
if (!(n % 23) || !(n % 29) || !(n % 31) || !(n % 37) || !(n % 41)) return 0;
if (check(2,n)) return 0;
if (check(3,n)) return 0;
if (check(5,n)) return 0;
if (check(7,n)) return 0;
if (check(11,n)) return 0;
if (check(13,n)) return 0;
if (check(17,n)) return 0;
if (check(19,n)) return 0;
if (check(23,n)) return 0;
if (check(29,n)) return 0;
if (check(31,n)) return 0;
if (check(37,n)) return 0;
if (check(41,n)) return 0;
return 1;
}请记住这个算法 并在尝试质因数分解前进行一遍素性检测
Trial division
最朴素的算法 我们枚举小于等于$\sqrt{n}$的数 然后进行分解 这个复杂度是$O(\sqrt{n})$ 当然 在合数中的表现普遍优于这个复杂度
接下来我们给出实现:
map<int,int> fac;
for (int i = 2; i * i <= n; i++)
{
while (!(n % i))
{
n /= i;
fac[i]++;
}
}
if (n != 1) fac[n]++;到此 我们解决了FACT0 这只是梦的开始(
Wheel factorization
这是对于朴素算法的一个小优化 我们发现我们所枚举的数其实只有$\frac{1}{2}$是有用的 所以我们可以得到这个实现:
map<int,int> fac;
while (!(n % 2))
{
n /= 2;
fac[2]++;
}
for (int i = 3; i * i <= n; i += 2)
{
while (!(n % i))
{
n /= i;
fac[i]++;
}
}
if (n != 1) fac[n]++;这个算法依然是$O(\sqrt{n})$ 这只是常数上的优化
Precomputed primes
上面这个算法优化的方式给了我们启发 我们可以打出一张素数表来 然后每次跳素数的倍数来优化我们的复杂度:
int pri[N],cnt = 0;
bool vis[N];
map<int,int> fac;
for (int i = 2; i < N; i++)
{
if (!vis[i]) pri[++cnt] = i;
for (int j = 1; j <= cnt && i * pri[j] < N; j++)
{
vis[i * pri[j]] = 1;
if (!(i % pri[j])) break;
}
}
for (int i = 1; i <= cnt && pri[i] * pri[i] <= n; i++)
{
while (!(n % pri[i])) mp[pri[i]]++,n /= pri[j];
}
for (int d = pri[cnt] + 1,i = 0; d * d <= n; d += pri[++i])
{
while (!(n % d))
{
n /= d;
fac[d]++;
}
if (i == cnt) i = 0;
}
if (n != 1) fac[n]++;这个的复杂度嘛 不太会算(神仙教我
Fermat's factorization method
费马的方法基于一个简单的平方差: $$ n=a^2-b^2\\ n=(a+b)(a-b)\\ \text{那么假设}n=dc\\ n=(\frac{c+d}{2})^2-(\frac{c-d}{2})^2 $$ 我们的思路是枚举$a$然后计算$b$ 在递归处理$c$和$d$
int fermat(int n) {
int a = ceil(sqrt(n));
int b2 = a * a - n;
int b = round(sqrt(b2));
while (b * b != b2) {
a = a + 1;
b2 = a * a - n;
b = round(sqrt(b2));
}
return a - b;
}但是费马算法在普通情况下的表现甚至不如朴素算法优秀 但是这个算法依然可以使用Wheel factorization 以及 Precomputed primes 进行一定的优化我不想写
而这个算法让我们把问题有了一定的转化 我们可以讲分解质因数的任务转化成一个寻找非平凡因子的问题 然后递归处理
Pollard's rho algorithm
Linux自带的factor中所使用的算法 期望复杂度在$O(n^{\frac{1}{4}})$ 算法导论上说是$O(\sqrt{p})$ $p$是$n$的最小质因子
我们考虑把一个数分解成两个数乘积的形式:$n=pq$
这个$p$和$q$我们可以考虑递归处理 代码大致如下:
void fac(int n)
{
if (isprime(n)) return ;
int p = find(n);
fac(p);
fac(n / p);
}我们最关键的问题在于如何找到这个$p$
简单的试除法显然并不满足我们的要求 我们需要一个更好的方法 考虑求$gcd$
我们假设有了一个数$x$ 那么$gcd(x,n)$一定是$n$的一个约数 假设我们找到了这样的一个非平凡约数 那么我们就可以把它当作$p$来递归处理了
问题是我们如何来寻找这个$x$呢
根据生日悖论我们可以知道组合取样可以有效地提高我们的效率 所以我们考虑生成一个随机的序列:$x_1,x_2,\dots,x_k$
我们所要选择的$p$是选择$1\leq i,j \leq k,p=gcd(|x_i-x_j|,n)$
我们如果真的随机生成了$k$个随机数序列 那我们的这个选取的最劣的情况需要$k^2$次 即两两枚举$i,j$然后进行计算 这样的复杂度并不太能接受
考虑一个伪随机的生成函数: $$ f(x)=(x^2+c)\ mod\ n $$ 可以顺便说一句的是 这个函数就是曼德勃罗集 Chaos的特性有效保证了这个函数的随机性
这个函数的图像大概是这个样子的经典图片:

我们给他一个初始值$x_0$ 通过$x_i=f(x_{i-1})$可以得到一个伪随机序列
我们可以选定一个$x_0$和$c$来得到我们随机的序列
在这个序列上 由于足够随机我们可以直接找相邻的两点进行作差 得到我们的$p$
这个代数序列上的枚举 我们可以观察到形状类似于$\rho$所以我们可以使用Cycle detection来进行随机数的选取
具体地一般有两种方法:Floyd's cycle-finding algorithm和Brent's algorithm
Floyd's cycle-finding algorithm
Floyd的这个算法据说是民间算法/? 不管
我们考虑一下存在一个循环的条件是:对于任意整数$i\geq \mu,k\geq 0$ 有$x_i=x_{i+k\lambda}$ 其中$\mu$是循环的起始位置 $\lambda$是循环的长度
那我们拿一个双指针 第一个双指针$p_1$一步走$1$ 第二个双指针$p_2$一步走$2$ 那么倘若$x_1\neq x_2$ 那么两个指针一定会在相遇 且第一次相遇的点到循环终点的距离和起点到循环起点的距离相同
证明是小学二年级就学过的行程问题 略
Brent's algorithm
这个算法的思想同样是双指针 不同的是采用倍增判断每次跳2的幂次来寻找我们上面提到的$\mu$和$\lambda$
我们在Pollard's Rho中更常用的是Brent's algorithm 因为不难证明的是 这种做法的比较次数不高于 Floyd's cycle-finding algorithm 而这个每次比较我们都需要进行一次$\gcd$ 所以使用这个算法可以有效减小我们的常数
最后让我们来看一下这个Pollard's Rho的实现吧:
int Pollard_Rho(int x)
{
int s = 0,t = 0;
int c = (int) rand() % (x - 1) + 1;
int step = 0,goal = 1;
int val = 1;
for (goal = 1;; goal <<= 1,s = t,val = 1)
{
for (step = 1; step <= goal; ++step)
{
t = f(t,c,x);
val = mul(val,abs(t - s),x);
if ((step % 127) == 0)
{
int d = gcd(val,x);
if (d > 1) return d;
}
}
int d = gcd(val,x);
if (d > 1) return d;
}
}
void fac(int x,int num)
{
if (x < 2) return ;
if (Miller_Robin(x))
{
maxx = max(maxx,x);
return ;
}
int p = x;
while (p >= x) p = Pollard_Rho(x);
int tmp = 0;
while ((x % p) == 0) x /= p,tmp += num;
fac(x,num);
fac(p,tmp);
}其实我的Pollard's Rho就是照着OI-wiki打的
到此 可以去先写一下FACT1
Algebraic-group factorisation algorithm
高质量好算法(?)
这部分算法主要有三个Pollard's p − 1 algorithm Williams's p + 1 algorithm Lenstra elliptic-curve factorization
我们从比较熟悉的开始讲起
Pollard's p - 1 algorithm
这个发明者和上面那个Pollard's Rho是一样的 但是做法很不像 这个是基于代数群分解的
我们从费马小定理出发: $$ a^{p-1}\equiv1\mod p\\ a^{(p-1)^k}\equiv a^{k(p-1)} \equiv 1\mod p $$ 所以对于任意$p-1|x$ 有$a^x\equiv 1\mod p$ 也就是$p|gcd(a^x-1,n)$
也就是我们可以得到一个$p$是$n$的一个因数了
显然 当 $$ x=\prod_{p\in prime,p\leq B}p^{\lfloor\log_pB\rfloor} $$ 时 我们可以一次验证足够多的数 得到我们想要的答案
当然 这个$B$是不断在变化的
让我们来看一下算法流程:
- 选定一个$B$ 计算$x$ 选定一个$a$
- 计算$g = gcd(a^x-1,n)$
- 如果 $g = 1$ 那么调大$B$ 返回步骤 $2$ 或者分解失败
- 如果 $g = n$ 那么减小$B$返回步骤 $2$ 或者分解失败
- 得到一个非平凡因子$g$
但是这个算法在一些数上是无法生效的 当一个数的存在两个素因子$p$和$q$满足$p - 1$的最大素因子和$q - 1$的最大素因子相等时 这个算法并不能帮我们分解
所以这个算法并不是正确的算法 我们可以定义他的复杂度是$\frac{T(n)}{P(n)}$ 即渐近时间除以渐近概率
复杂度是: $$ T(n)=O(B\log B\log^2n)\\ \text{而被分解的概率是}B=\sqrt[a]{n},P(n)=a^{-a}\\ \text{复杂度是}e^{(1+o(1))\sqrt{\log n\log\log n}} $$ 具体地证明这个复杂度的话 我们可以发现在进行Miller-Rabin后最小的质因子一定不会大于$\sqrt{n}$
说句闲话 由于这个算法的优秀复杂度 所以在原来的密码学中 有安全素数这个术语 即用无法使用这个算法进行分解的数来进行加密
这不是一个正确算法 但是还是能帮助得到一些启示 让我们把这个问题转化到代数群上考虑
这个算法的本质是在模$p$意义下的群$(\mathcal Z,\times)$ 我们记作$F_p$中 任何子群的阶都是$p-1$的因数 且任何两个不同的$\mathcal F_p$和$\mathcal F_q$中 $a^{p-1}$和$a^{q-1}$不同 所以我们可以把$p$和$q$提取出来
换句话讲 考虑我们实际上是把数分解成:$n=ab$而$B$是我们分辨$a$和$b$的阀门 若$\varphi(a)$是一个B-smooth数 但是$\varphi(b)$不是 那么我们救可以把$a$和$b$区分
事实上我们可以换一些群 在 Williams's p + 1 algorithm 中就是构造了一个代数群 和这个算法非常相似 应用也不多 不再过多介绍
Lenstra elliptic-curve factorization
这是本文最劲爆的内容了 觉得前面的内容简单的可以重连了觉得简单的不要声张
这个算法知道的人现在应该也不少了qaq
在Pollard's p - 1中 会失败的主要原因是群的阶是$p - 1$ 而这个数可能不是powersmooth的
自然数$n$被称之为B-smooth 当且仅当$n$的任何质因数$p$满足$p\leq B$
而B-powersmooth 则是指所有可以整除$n$的形如$p^q$的数 其中$p$为质数 满足$p^q\leq B$
这个问题在于我们选择群 所以我们要考虑更换我们的算法所用到的群
众所周知 椭圆曲线上的点构成了一个$(\{(x,y)|x,y\in R\},+)$的群
椭圆曲线
椭圆曲线是以下形式的方程的曲线:
$$
E:\ y^2=x^3+ax+b
$$
特别地 我们的椭圆曲线不能有奇点 一般地 我们表示成椭圆的判别式:
$$
\Delta=-16(4a^3+27b^2)\neq0
$$
一般地 我们还有当$\Delta>0$时 曲线有两个联通分量 当$\Delta<0$时 曲线只有一个联通分量 便于理解给出了一幅Geogebra画的图虽然和我们的主题关系并不大

我们定义一个无穷远点$O$在$E$上 定义点$A'$是点$A$关于$x$轴对称的点
定义在$E$上的两点的加法:
在下图中$A+B=C'$
即从两点$A$和$B$引出的直线和椭圆曲线的第三个交点关于$x$轴的对称点
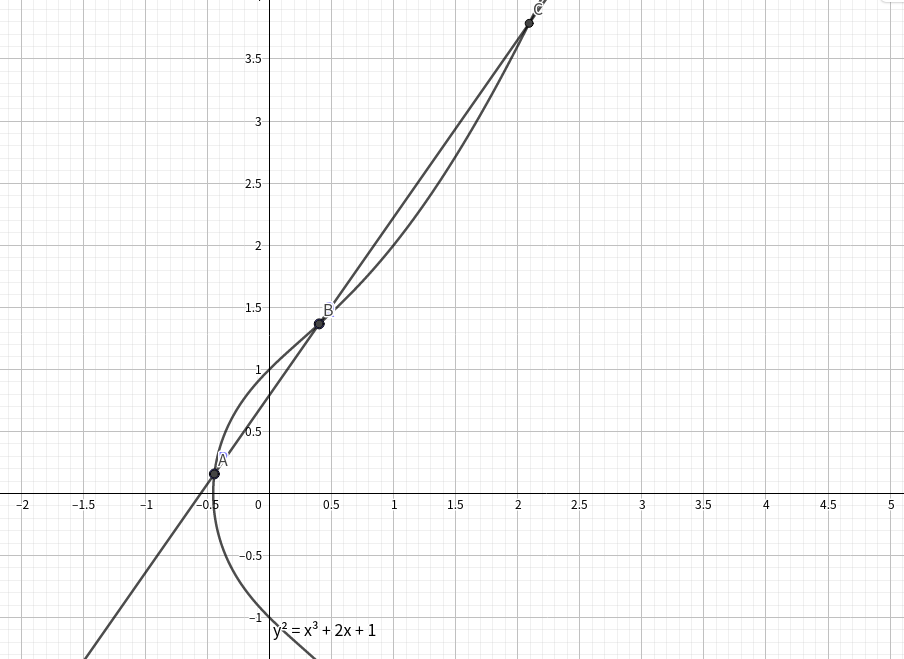
我们不难发现我们定义的$O$是这个运算的单位元 即$A+O=O+A=A$
而当$A=B$且$A$为拐点的时候我们定义$A+A=A'$
不难发现这个群是一个阿贝尔群
对于椭圆点上的有理点 和这个运算依然能构成一个群 然而有理域依然无法帮我们很好地解决问题 所以我们尝试缩小到一个有限域$\mathcal F_n$ 从而得到一个映射平面$(\mathcal Z / n,\mathcal Z)$ 此时的点$O$我们认为是含有$p^x,x>1$因子的坐标: $$ (x_1,y_1)+(x_2,y_2)=(u,v)\\ s=\frac{y_2-y_1}{x_2-x_1}\\ \text{当}x_1=x_2\text{时},(u,v)=O\\ u=s^2-x_1-x_2,v=y_1+s(u-x_1)\\ \text{考虑令}x_1=x_2,y_1=y_2,s=\frac{3x^2+a}{2y}\\ \text{那么}(x,y)+(x,y)=(s^2-2x,y+s(s^2-3x))\\ \text{当}y=0,(x,y)+(x,y)=O $$ 而当在模$n$意义下出现点$O$的时候 必然出现了一个点不存在乘法逆元 也就找到了一个非平凡因子 这个问题就可以得到递归解决了
详细介绍一下算法流程:
- 选取一个椭圆曲线$E$和上面在群中的一个元素$P=(x,y)$
- 选定一个值$B$ 这和Pollard's p - 1很类似 对于$10^{30}$位左右的数 我们一般选取$700$
- 计算$\left(\displaystyle\prod\limits_{p\in prime,p
- 在加法求逆的过程中 寻找点$O$
复杂度分析类似于Pollard's p - 1 我们当$|(\mathcal Z / n,\mathcal Z)|$是B-smooth的时候停下 复杂度是:$O(B\log^2n)$ 终止概率一样是$B=p^\frac{1}{a},P=a^{-a}$
所以$T(n)=e^{(\sqrt{2}+o(1))\sqrt{\log p\log\log p}}$ $p$是$n$最大的因子
到此 我们可以解决FACT2

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号